仍然是写给科博馆的,器象 | 事先做好——纳皮尔的算筹和对数的共同逻辑。
约翰•纳皮尔(John Napier,1550-1617)出生于苏格兰的名门望族,他继承了家族的财富,经营着自己的城堡和庄园。他以研究的态度来打理他的土地,对肥料等问题做了实验和分析。他也是一个虔诚的新教徒,为了反击天主教,他积极介入当时的宗教争论,并撰写了颇有影响的神学著作。他也是一个巫师,他精心喂养了通灵的黑公鸡,并且出门时常常带着黑蜘蛛。他还为了抗击西班牙人,设计了火炮和战车等军事装备……
天文学、占星学和数学方面的研究,只是纳皮尔这位庄园主业余爱好的一小部分,但却在后世产生了最大的影响。他因此被誉为史上最伟大的苏格兰数学家之一。
纳皮尔在数学上最大的成就就是发明了“对数”,同时,他在三角函数和球面三角等领域也有贡献,还规范了小数点的记法。另外,他所发明的“纳皮尔筹”,作为一种计算乘法的辅助工具,也被认为是现代机械计算器的先驱。


“纳皮尔筹”(Napier’s Bone),直译是“纳皮尔的骨头”,这是因为早期这种算筹经常用象牙制作而得名。这种算筹的原理并不复杂,来源是所谓的“格子乘法”。
格子乘法很可能源于印度,在中世纪阿拉伯人那里就流传开来,后来也传入欧洲和中国,在中国明代叫做“铺地锦”。本质上无非是一种笔算的技法,方法如下:
把乘数和被乘数分别横着写在顶部和竖着写在右侧,每一位数对应一格,绘制出一个带斜线的方格组成的矩形,然后把多位数相乘先拆分为若干个一位数相乘,比如135×79,就分别计算1×7、3×7、5×7、1×9、3×9、5×9,填入由纵横坐标确定的相应格子中。一位数乘法只要背乘法口诀即可,结果也不会超过两位数,于是就把十位数填入由斜线分割的左上格,把个位数填入由斜线分割的右下格(左图)。然后再沿斜线方向做加法,把每一斜线的数字自右上至左下加起来——和一般的竖式加法一样,需要计算进位——填在最后。这样最后加得的结果,就是所求的乘积了。
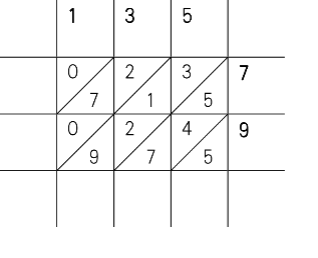
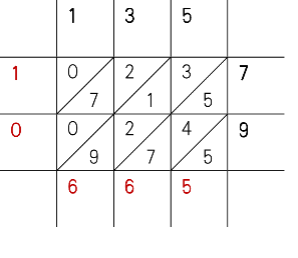
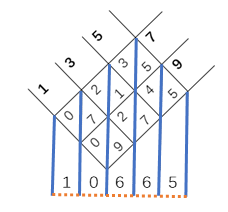
简单来说,格子乘法的实质就是把多位数乘法问题拆分为若干一位数的乘法和加法问题。利用稍微复杂一些的方式,还可以用类似方法计算除法、乘方和开方等。那么纳皮尔的算筹相对于格子乘法的改进在哪里呢?正如我们的展品介绍所说:“纳皮尔只不过是把格子乘法里填格子的工作事先做好而已”。
纳皮尔算筹预先在相应位置填好了一位数乘法的结果,这样在处理简单的多位数乘一位数时,可以几乎不需要笔算而直接读写出答案,在计算多位数乘多位数时,也可以减少动笔的频率和避免简单的抄写错误。
但不要低估这个“事先做好”的意义。这既是纳皮尔算筹的意义,也同样是纳皮尔之所以发明对数的诀窍。
什么是对数?今天我们都知道,对数就是指数的逆运算,比如ax=N,那么loga N=x。但是,纳皮尔并不是这样理解对数的。事实上,这是数学史上一件颇为神奇的事情——对数的发明比指数更早。
直到纳皮尔死后二十多年,笛卡尔才以一个比较现代的方式定义了指数运算,而直到整整一百五十年后,才由欧拉明确论证了指数与对数的互逆关系。
那么我们现代人就很纳闷了,在没有建立指数的概念的时候,纳皮尔所发明的对数究竟是一个什么东西呢?
首先我们要理解指数为什么那么晚才被认识。这是因为在古代数学家眼中,乘法总是应当有某种几何意义的。比如,a、b如果是两个“数”,那么a×b表示a行b列的总数,如果a、b是两个“量”,那么a×b表示一个长a宽b的矩形的面积。类似地,“平方”表示一个正方形的面积,“立方”表示一个立方体的体积。但更高的幂次,或者幂次为负数或小数的话,就压根没有恰当的表达方式,也没有合理的物理学或几何学的意义。
指数符号的发明和接受,依赖于整个近代数学不断酝酿的一个基本变革,就是符号的抽象化。现代数学家不再要求数学符号有某个明确的指称,不要求数学式子有一个真实的意义。符号的意义完全由其运算规则所赋予,而不再依附于任何现实的形象。这样一来,包括指数在内,无理数、负数、虚数、无穷小量等各种现代数学概念,才变得容易接受了。
在符号的抽象化、中立化的历程中,笛卡尔扮演了关键角色,他的解析几何最终颠倒了代数与几何的古老关系,从而使得脱离几何意义的高次指数成为可能。
而纳皮尔发明对数却并不是在符号的抽象化这一思路下展开的。纳皮尔的对数本质上是一种辅助计算的技艺或手段。
纳皮尔在其介绍对数的著述中,开篇就谈及他的动机,他说道:“在数学实践中,最麻烦的事情莫过于对大数进行乘法、除法、平方或立方等计算了,除了要在枯燥乏味中浪费时间之外,还经常会手滑算错。于是我开始思考,可以用某些确定而准备好的技艺(certain and ready art)来消除这些麻烦。”
出自纳皮尔1614年的著作Mirifici logarithmorum canonis descriptio,转引于https://mathshistory.st-andrews.ac.uk/Biographies/Napier/
我们看到,这一动机是对数与算筹共通的,我们也完全可以把纳皮尔筹理解为他所说的为了解决大数乘除法等问题而发明的“准备好的技艺”。
在纳皮尔那里,对数指的无非是两组数列的对应关系,比如:
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | …… |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | …… |
在这两行数之间存在一一对应的关系,而同时,第一行中的乘除法恰好对应于第二行中的加减法。比如说,在第一行中,我们把第2列和第3列的两个数相乘,得到的是第5列的数(4×8=32),而在第二行中,我们同样找到第2列和第3列的两个数,把它们加起来,就恰好也会得到第5列的数(2+3=5)。
在构建这两行数列的时候并不必然需要指数的概念,而是完全可以按照后一个数是前一个数乘以2,这样按部就班的方式,实践性地预先列出非常大的数表。然后,纳皮尔把这两条数列不是看作间断的整数,而是看作连续的“量”,但第一行数值与第二行数值之间的一一对应关系,以及乘法对应加法的关系保持不变。
接下来的事情就是“事先做好”足够长的“数列”,填入足够多的“数值”,这样一来,当我们要做某两个大数的乘除法时,就先在第一行找到这两个数值,然后在第二行中找到相对应的两个小得多的数值,对第二行的两个数值做加减法,在第二行中找到加减的结果,再去找到对应第一行中的数值,那就是所求乘除法的结果了。
“对数”这门通过“事先做好”的数值对应关系,来辅助进行大数计算的“准备好的技艺”,很快流行开来,被苦于数值计算的科学家和计算者接受。后来产生的各式“计算尺”、“比例规”,都是基于对数及其思想的工具。直到早期的一些电子计算器仍然借助对数来计算乘除法,因此有时会出现2×2=3.99999…之类的结果。
这种“事先做好”的思路指引了整个西方近代计算器具的发展历程。正如对数先于指数,在推动现代技术发展的动力方面,实用需求经常比概念的建立更加重要。现代数学家部分接受了商人的态度,从而打破了希腊数学家对理念世界的固执,促进了数学与机械的结盟。




