用Excel展演浑沌!
用于科普,借助Excel演示浑沌的好处是显而易见的:首先,Excel是一个“家常”的软件,几乎每台电脑上都有,不需要使用者专门下载分形软件,随手就来。而且,Excel的操作是傻瓜式的,不需要任何编程技巧。同时,Excel生成图形非常方便,转换为图片、Word文档、PPT、网页文件等都非常便捷。对于初次接触分形的人来说,用Excel亲手操作显然是最直接的体验方式。
在绘制较简单的图样时,Excel的操作相当便捷。以“国王映射”的最初形式为例:
x_(n+1)=sin(by_n)+csin(bx_n),
y_(n+1)=sin(ax_n)+dsin(ay_n),
先在Excel空白工作表的第一行的单元格中依次键入a、b、c、d、x0、y0的数值,例如在A1、B1、C1、D1、E1、F1中分别填入-1,3,0.7,0.7,0.1,0.1
在第二行前四个单元格,也就是对应常数的下方依次键入“=A1”、“=B1”、“=C1”、“=D1”,这样做的好处是方便经常改换常数。
在第二行的后两个单元格,即E2、F2中,填入x_n和y_n的第一次递推公式:
即在E2中键入“=SIN(B2*F1)+C2*SIN(B2*E1)”——注意其中B2、C2分别等于b、c。
在F2中键入“=SIN(A2*E1)+D2*SIN(A2*F1)”。
然后选中第二行的6个单元格,将鼠标移至选择框右下角,当鼠标指针变为十字形时按下拖曳,一直往正下方拖动,可拖至10000行甚至更多,至多可达65536行。拖动的速度是很快的,完成后按ctrl+Home可以方便地回到回到第一行。
选中E、F两列,点击常用工具栏上“图表向导”按钮,或“插入”菜单——“图表”。
选择“XY散点图”,直接Enter或点“完成”即可!
生成的默认图表视觉效果不够理想,拖动图表边框将其拉大(不妨拉到数百行那么长),然后改变窗口的显示比例(比如在点选任一单元格时按住ctrl同时滑动鼠标滚轮),调节到适合状态即可。
在图表中点击右键,选择“图表选项”,可以去除不必要的网格、X轴、Y轴、图例等。双击背景可去除背景颜色,或选择合适的颜色;双击任一数据点可以调整数据点的大小、形状和颜色。
图样即绘制完毕!
接下来可调整常数a、b、c、d和x、y的初始值以观察图案的变化,只需要在第一行操作即可。
也就是说一旦改变了第一行相应的a、b、c、d、x0、y0的数值,整张数据表以及生成的图案就会即时改变!
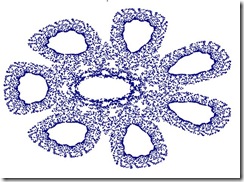
下面附上的是我用上述方法生成的图样(共30000余点)
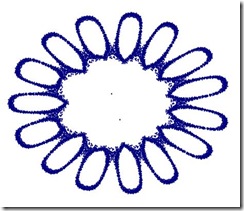
修改各常数可得到完全不同的图样!比如将第一行改为-1.05,2.29,1,-1,0.1,0.1,得到下图:
2006年4月28日
用Excel展演浑沌增补:变形金刚&三翅鹰
星定 发表于 2006-04-28 20:48:55
———————————————————————————————
根据原始文本重新录入
科哲作业原始版本:
受到陈星群同学的启发领悟到了用Excel演示混沌的技巧,非常好用,特尝试之~
他做了第一题,我便做第二题:外加做了一些国王映射等图形。
Xn+1=μXn(1-Xn)
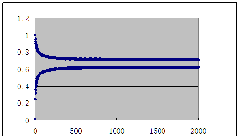
当μ约在(0,0.75)之间,取任意初值,得到周期1。
下仅举μ=0.7,X1=0.01时图像为例:
当μ约在(0.75,1.25)之间,得到周期2。
下举μ=0.751,X1=0.01时图像为例:
再举μ=1.2,X1=0.01时图像为例:
当μ约在(1.25,1.37)之间,得到周期4。
下举μ=1.3,X1=0.01时图像为例:
当μ约在(1.37,1.4)之间,周期开始变得复杂起来。
下举μ=1.4,X1=0.01时图像为例:
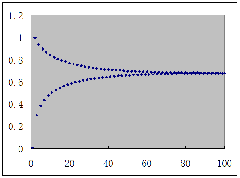
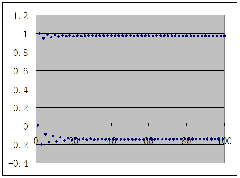
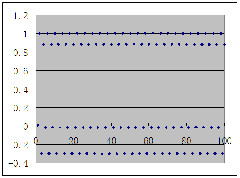
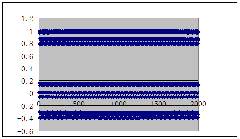
当μ约在(1.4,2)之间时,出现混沌!
下举μ=2,X1=0.01时图像为例——以下分别为取到X100、X10000时的视图:
另外,使用Excel,只要同时列两组递归数列,使用“无数据点平滑散点图”,也可以画出二维的混沌图来,例如将本题的递归公式错开一位写,即点An=(Xn,Xn+1),便可得到形如下图的图样:
依此法应该可以与使用编程造出更复杂的花样来。
下图由
Xn+1=1-aXn2+Yn,Yn+1=bXn,X1=Y1=1,a=0.1,b=1生成
下图由
Xn+1=1-aXn2+Yn,Yn+1=bXn,X1=Y1=0.5,a=0.134,b=1生成
下图为Xn+1=sin(bYn)+csin(bXn),,Yn+1=sin(aXn)+dsin(aYn),a=-1.5,b=2.6,c=0.86,d=0.75,X1=Y1=0.5的图形(取10000点):
下图为Xn+1=sin(bYn)+csin(bXn),,Yn+1=sin(aXn)+dsin(aYn),a=-1,b=3,c=0.7,d=0.7,X1=Y1=0.1的图形(取10000点):
Xn+1=sin(aYn)-zcos(bX n),
Yn+1=zsin(cXn)-cos(dY n),
Zn+1=esinXn.
其中a=2,b=3.281,c=-0.5975,e=0.6666,X0=1.41,Y0=2,Z0=1,时(X、Y)的花样(10000点)
用Excel展演浑沌!(加强版)
用于科普,借助Excel演示浑沌的好处是显而易见的:首先,Excel是一个“家常”的软件,几乎每台电脑上都有,不需要使用者专门下载分形软件,随手就来。而且,Excel的操作是傻瓜式的,不需要任何编程技巧。同时,Excel生成图形非常方便,转换为图片、Word文档、PPT、网页文件等都非常便捷。对于初次接触分形的人来说,用Excel亲手操作显然是最直接的体验方式。
在绘制较简单的图样时,Excel的操作相当便捷。以“国王映射”的最初形式为例:
x_(n+1)=sin(by_n)+csin(bx_n),
y_(n+1)=sin(ax_n)+dsin(ay_n),
先在Excel空白工作表的第一行的单元格中依次键入a、b、c、d、x0、y0的数值,例如在A1、B1、C1、D1、E1、F1中分别填入-1,3,0.7,0.7,0.1,0.1
在第二行前四个单元格,也就是对应常数的下方依次键入“=A1”、“=B1”、“=C1”、“=D1”,这样做的好处是方便经常改换常数。
在第二行的后两个单元格,即E2、F2中,填入x_n和y_n的第一次递推公式:
即在E2中键入“=SIN(B2*F1)+C2*SIN(B2*E1)”——注意其中B2、C2分别等于b、c。
在F2中键入“=SIN(A2*E1)+D2*SIN(A2*F1)”。
然后选中第二行的6个单元格,将鼠标移至选择框右下角,当鼠标指针变为十字形时按下拖曳,一直往正下方拖动,可拖至10000行甚至更多,至多可达65536行(但绘图时最多只能用到32000个数据点)。拖动的速度是很快的,完成后按ctrl+Home可以方便地回到回到第一行。
选中E、F两列,点击常用工具栏上“图表向导”按钮,或“插入”菜单——“图表”。
选择“XY散点图”,直接Enter或点“完成”即可!
生成的默认图表视觉效果不够理想,拖动图表边框将其拉大(不妨拉到数百行那么长),然后改变窗口的显示比例(比如在点选任一单元格时按住ctrl同时滑动鼠标滚轮),调节到适合状态即可。
在图表中点击右键,选择“图表选项”,可以去除不必要的网格、X轴、Y轴、图例等。双击背景可去除背景颜色,或选择合适的颜色;双击任一数据点可以调整数据点的大小、形状和颜色。
图样即绘制完毕!
接下来可调整常数a、b、c、d和x、y的初始值以观察图案的变化,只需要在第一行操作即可。
也就是说一旦改变了第一行相应的a、b、c、d、x0、y0的数值,整张数据表以及生成的图案就会即时改变!
下面附上的是我用上述方法生成的图样(共30000余点)
2006年4月28日
修改各常数可得到完全不同的图样!比如将第一行改为-1.05,2.29,1,-1,0.1,0.1,得到下图:
再看一个非常有趣的图样——ZZSUC映射(但我做不出理想中的图样,可能是弄错了,不过我搞出的东西也蛮好玩的~~):
x_(n+1)=(x_n+Ksiny_n)cos(2π/q)+y_nsin(2π/q)
y_(n+1)=-(x_n+Ksiny_n)sin(2π/q)+y_ncos(2π/q)
在第一行依次输入K、X0、Y0、q的初始值。
在第二行依次输入“=A1”、“=(B1+A2*SIN(C1))*COS(2*PI()/D2)+ C1*SIN(2*PI()/D2)”、“=(B1+A2*SIN(C1))*SIN(2*PI()/D2)+ C1*COS(2*PI()/D2)”、“=D1”,按前述方法,做B、C两列的图样。
我们取X0=-1,Y0=1。
q为3至6的整数。
注意生成的图形对K极为敏感。下依次举q=4时,K为1.667、1.667000000001、1.667000000002、2.05这四种情况的图样(10000点):
我们看到,当不断调整K时,q=4的图案简直像玩“变形金刚”那样,千变万化——第4幅图的形状简直就象变形金刚!!。不断调整参数值那个“变形金刚”还会变飞机呢(2.0499999999)!
但是需要指出的是,这里看到的形状变化在某种意义上只是个假象,因为其形状与所取的点的个数直接有关,似乎取的点越多,这个映射是会延展直整个平面的。下面对那个变形金刚中的后5000个数据点用另一种颜色进行染色(这也是用Excel做的,只是多加了一行数据让它在5000行后“=Bi”
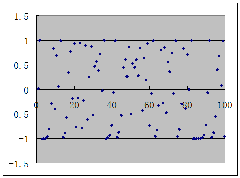
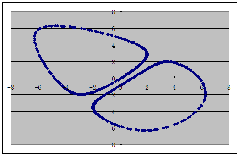
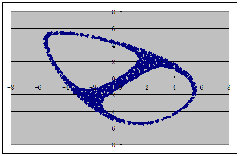
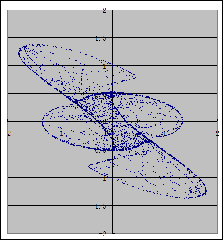
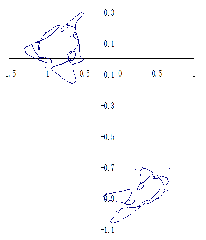
最后做传说中的“三翅鹰映射”:
我在第一行A1~G1依次输入:
1,1,-0.6,0.95,=2-2*C1,=C1*A1+E1*A1*A1/(1+A1*A1),=A1
在第二行A2~H2依次输入:
=D1*B1+F1,=F2-G1,=C1,=D1,=2-2*C2,=C1*A2+E1*H2/(1+H2),=A2,=A2*A2
然后依前法拖曳第2行至上万行,对A、B两列做图表:
第一行的前两个单元格分别为X和Y的初值,对之调整几乎没有影响,而C1、D1两格为常数,对之调整将剧烈影响图样。
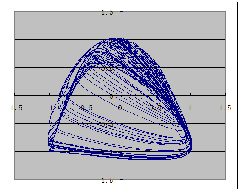
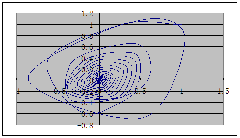
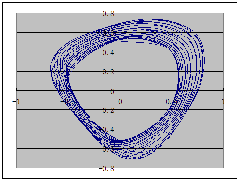
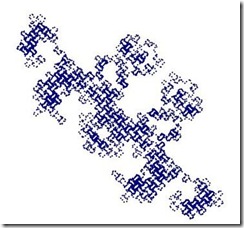
下面给出三翅鹰映射图样及其若干变种:




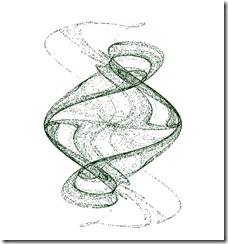

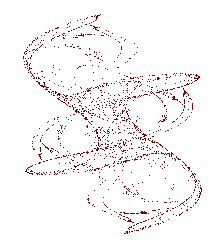
![clip_image004[4] clip_image004[4]](https://yilinhut.net/wp-content/uploads/2011/02/clip_image0044_thumb.jpg)
![clip_image006[4] clip_image006[4]](https://yilinhut.net/wp-content/uploads/2011/02/clip_image0064_thumb.gif)
![clip_image010[4] clip_image010[4]](https://yilinhut.net/wp-content/uploads/2011/02/clip_image0104_thumb.gif)
![clip_image012[4] clip_image012[4]](https://yilinhut.net/wp-content/uploads/2011/02/clip_image0124_thumb.gif)
![clip_image014[4] clip_image014[4]](https://yilinhut.net/wp-content/uploads/2011/02/clip_image0144_thumb.gif)
![clip_image016[4] clip_image016[4]](https://yilinhut.net/wp-content/uploads/2011/02/clip_image0164_thumb.gif)
![clip_image020[4] clip_image020[4]](https://yilinhut.net/wp-content/uploads/2011/02/clip_image0204_thumb.gif)
![clip_image022[4] clip_image022[4]](https://yilinhut.net/wp-content/uploads/2011/02/clip_image0224_thumb.gif)
![clip_image024[4] clip_image024[4]](https://yilinhut.net/wp-content/uploads/2011/02/clip_image0244_thumb.gif)